You’ll walk alone

Bei vielen Entscheidungen, die wir treffen, geht es um die Abwägung von Einzel- und Gruppeninteressen. Allen kann man es nicht Recht machen; aber man kann Modelle definieren, die so gestaltet sind, dass sie von allen akzeptiert werden können und zwar dann, wenn mit erreichten Vorteilen auch Nachteile in Kauf genommen werden. Bei weihnachtlichen Aufräumungsarbeiten ist mir wieder ein Programm in die Hände gefallen, das ich zur Simulation der Warteschlangen für den Abo-Vorverkauf formuliert habe. Bereits im Mai 2015 wurde ein Vorschlag zur fairen Reihung von Abo-Anwärtern gemacht: Die besten Plätze für die besten Fans. Aber dabei wurden wohl zu viele Dinge berücksichtigt; es war zu kompliziert. Rapid hat daher ausschließlich die bisherige Abo-Vergangenheit als „Vordienstzeit“ herangezogen. Das Problem ist, dass derzeitige Sitzgemeinschaften durch die Art der Vergabereihenfolge zerrissen werden, weil die Abodauer nicht bei allen dieselbe ist. Eine Sitzgemeinschaft hat zwei Möglichkeiten:

• Das Modell „Einsamer Wolf“: jeder kauft sein Abo an dem ihm zugewiesenen Tag: die Gruppe wird zerrissen
• Das altruistische Modell: die Gruppe kauft am Einkaufstag des jüngsten Abonnenten: die älteren Abonnenten verzichten auf bessere Plätze zu Gunsten der Gemeinschaft

Nehmen wir zunächst an, dass jede Sitzgemeinsschaft beisammen bleiben will und dass jede dieser Sitzgemeinschaften ein neues Mitglied „mitnehmen“ möchte. Dann wird es am 4. April ein ziemliches Gedränge geben, denn das ist der Einkaufstag für „frischgfangte“ Abonnenten. Mein Vorschlag war, den Sitzgemeinschaften jenen Einkaufstag zuzuweisen, der der mittleren Abodauer der Gruppe entspricht. Treten also ein Vater (10-Jahres-Abonnent) und sein Sohn (2-Jahres-Abonnent) als Sitzgemeinschaft auf, dann können sie am Tag für 6-jährige Abonnenten einkaufen. (10+2)/2=6 In meiner Sitzumgebung gibt es praktisch nur solche Sitzgemeinschaften. Immer ist auch jemand dabei, der nicht ein „Ewig-Abonnent“ ist. Das Problem dieser Mittelung für Rapid ist (das wurde bei der Weihnachtsfeier der Fanklubs kommuniziert): es ist kompliziert und kaum administrierbar. Man muss das aber gar nicht besonders administrieren. Jemand kommt für seine Gruppe einkaufen und hat den Mittelwert vorher ausgerechnet und weiß also, an welchem Tag er kommen kann. Das einzige, was der Mitarbeiter im Fancorner tun muss: diese Rechnung an Hand der zugesendeten  Verlängerungs-Briefe nachvollziehen. Weil aber offenbar „der Zug abgefahren ist“, hat diese Beschreibung nur den Sinn einer Dokumentation. Vielleicht kann man ja eine solche Simulation in einem anderen Zusammenhang wieder einmal brauchen. Darum geht es also: fördert man die Gemeinschaft im Sinne eine „You’ll never walk alone“ oder muss man das „never“ streichen, so wie das jetzt der Fall zu sein scheint. Das Problem solcher „Gerechtigkeitsüberlegungen“ ist, dass wir nicht wissen, wie die Sitzgemeinschaften (=Gruppen) zusammengesetzt sind. Wir wüssten es, wenn wir alle einladen würden, sich per E-Mail als Sitzgemeinschaft zu deklarieren aber dazu fehlt wahrscheinlich das Personal – wenn man es händisch macht, natürlich. Es gibt aber anerkannte Verfahren, die der populären Namen „Monte-Carlo-Simulation“ haben, die gewisse Rückschlüsse liefern, auch wenn wir diese Gruppen nicht kennen. Das funktioniert so: alle Festlegungen erfolgen zufällig. Man legt eine Anzahl von Gruppen fest (man kann das wählen, im Bild sind es 100). Jeder Gruppe wird eine zufällige Anzahl von Mitgliedern (von 2 bis 10) und dann für jedes Mitglied eine zufällig Laufzeit zugeordnet. Jede Gruppe hat eine mittlere Abo-Laufzeit und das ist auch ihr gemeinsamer Einkaufstag. Die längeren Abonnenten verzichten auf Abozeiten, jüngere Abonnenten bekommen Zeiten dazu. Ein Mittelwert eben. Diese Gruppen findet man in der Online-Version der Simulation im Anschluss an die Zusammenfassung. Der Mittelwert jeder Gruppe ist grün hervorhehoben. Hier gibt es diese Simulation. 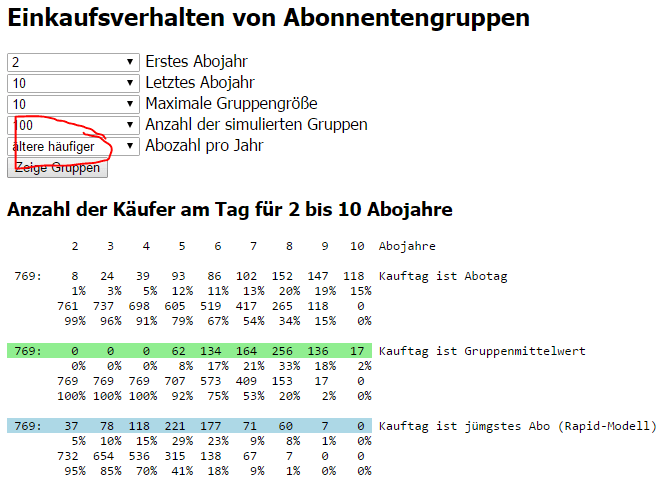Man kann an den Parametern „drehen“: http://ewkil.at/abogruppen.aspx Das Programm simuliert Abonnenten mit verschiedenen Abodauern und ordnet sie zehn verschiedenen Einkaufstagen zu. Man kann die Anzahl der Abojahre von 2 bis 10 einstellen. Gleichzeitig definiert das Programm Gruppen mit bis zu 10 Abonnenten, die verschiedene Abolaufzeiten haben. Wie diese Gruppen ausschauen, sieht man nach den zusammenfassenden Zeilen. Der grün markierte Zeitpunkt ist der Mittelwert der jeweiligen Gruppe.

Kauftag ist Abotag

Der Abschnitt „Kauftag ist Abotag“ zeigt, an welchem der neun Verkaufstage (2…10) wie viele Abonnenten einkaufen werden, wenn es keine Gruppenbildung gibt. Andy Marek kennt die Verteilung der „Abo-Vordienstzeiten“ sehr genau und hat erzählt, dass es viel mehr Langzeit-Abonennten gibt als Jung-Abonennten. Diesen Umstand kann man unter „Abozahl pro Jahr“ berücksichtigen. Die Voreinstellung ist daher „ältere häufiger“. Die ersten beiden Zeilen zeigen, an welchem Tag, wie viele von den 769 simulierten Abonnenten  einkaufen werden. Erste Zeile in absoluten Zahlen, die zweite Zahl in Prozenten. Die dritte und vierte Zeile zeigt, wie viele Käufer an diesem Tag bereits eingekauft haben. Man sieht, dass (wegen der größeren Anzahl älterer Abos) sich an den ersten Einkaufstagen mehr Einkäufer einstellen werden.

Kauftag ist jüngstes Abo

Im blauen Abschnitt „Kauftag ist jüngstes Abo“ wird gezeigt, was passiert, wenn eine Gruppe solidarisch ist und sich an dem jüngsten Abonnenten orientiert (das Rapid-Modell). Dann drängen sich die Käufer an den späteren Tagen zusammen.

Kauftag ist Gruppenmittelwert

In diesem Modell, wenn also die Gruppe an einem mittleren Tag einkauft, rücken die Käufer eher in die Mitte, die ersten und letzten Einkaufstage werden seltener frequentiert. Wichtig ist bei diesen Zahlen anzumerken, dass es hier nur um den Einkauf von Gruppen geht, Real wird es immer eine Kombination aus „Kauftag ist Abotag“ (entsolidarisierte Gruppen und „einsame Wölfe“) und eines der beiden anderen Modelle geben. Das Mittelwertmodell hat sehr hübsche Eigenschaften: Nehmen wir das Beispiel, dass drei Uralt-Abonnenten mit 10 Jahren Abodauer einen jungen Freund mitnehmen wollen, der noch keinen Aboplatz hatte. Mit dem Rapid-Modell kommen die nur so zusammen, indem die drei pokern. Sie kaufen zwei nebeneinander liegende Plätze, lassen dann einen Platz frei und kaufen den übernächsten dazu. Jetzt müssen sie hoffen, dass niemand diesen einen Platz kauft und ihr junger Freund kauft sich dann diesen Platz am letzten Einkaufstag. Nicht sehr kultiviert, wenn Ihr mich fragt. Beim Mittelwertsmodell rechnen wir: (10+10+10+0)/4 = 7.5~=8. Sie können daher entspannt und ganz ohne pokern am Einkaufstag für 8jährige Abonennten wählen.